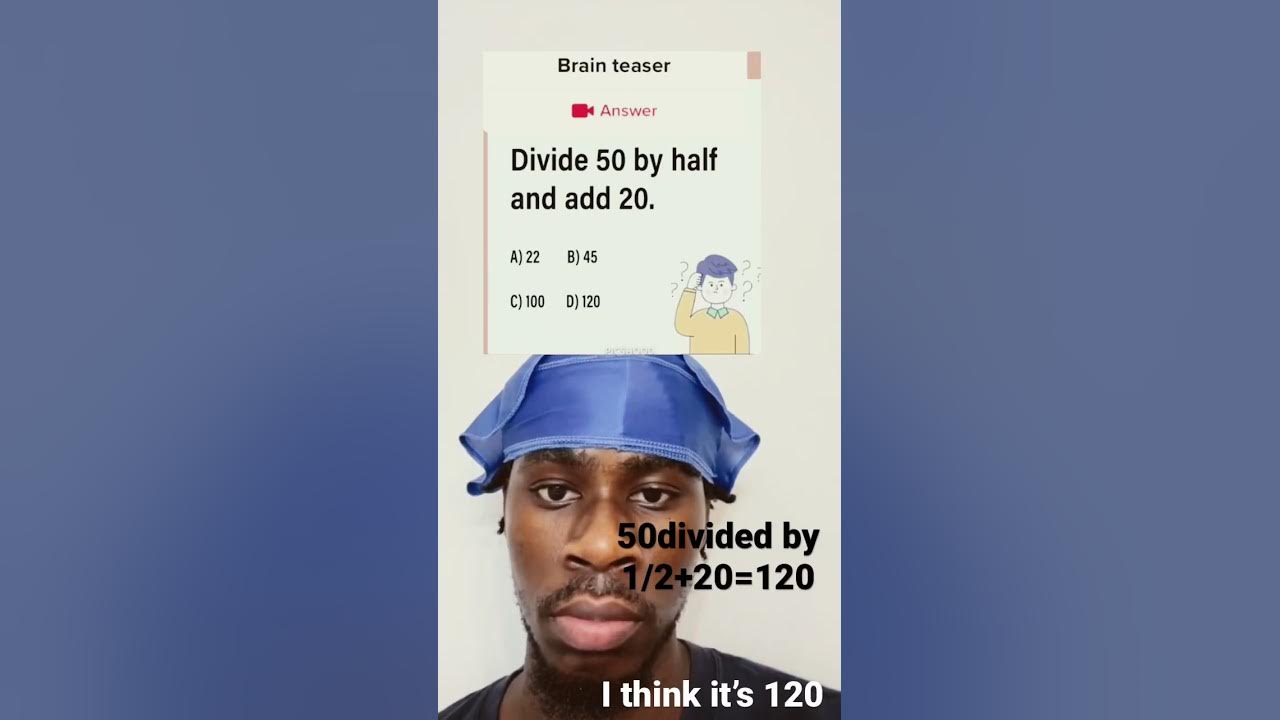
Mathematics often holds a special place in our lives, sometimes appearing simple and straightforward, and other times presenting intricate puzzles that make us scratch our heads. One such conundrum is the phrase, "divide 50 by half and add 20." This seemingly straightforward operation can lead to confusion if not approached correctly. So, let's embark on a journey to break down this mathematical expression, understand its components, and unveil the final answer.
At first glance, one might think that dividing 50 by half is simply halving the number. However, in mathematics, dividing by a fraction—like 0.5, which is equivalent to half—means you are effectively multiplying by its reciprocal. Therefore, dividing 50 by half involves a bit more calculation than meets the eye. Once we grasp this concept, we can then proceed to add 20 to the result, leading us to a fascinating conclusion.
In this article, we will explore the steps involved in solving the expression, "divide 50 by half and add 20," while also addressing some common questions that arise along the way. Whether you’re a student brushing up on your math skills or an adult curious about the nuances of mathematical operations, this exploration will provide clarity and insight into this intriguing calculation.
What Does "Divide 50 by Half" Really Mean?
To comprehend the operation "divide 50 by half," we need to revisit the basics of division. When we divide a number by a fraction, we actually multiply by the reciprocal of that fraction. So, in this case, dividing 50 by 0.5 is equivalent to multiplying by 2. This means:
- Divide 50 by 0.5 = 50 ÷ 0.5
- Which is the same as: 50 × 2 = 100
How Do We Add 20 to the Result?
After determining that dividing 50 by half results in 100, we can easily add 20 to this figure. The addition is straightforward:
- Result after division: 100
- Add 20: 100 + 20 = 120
Thus, when you “divide 50 by half and add 20,” the final answer is 120.
Why Do Many Get Confused by This Operation?
Many people stumble over the phrase "divide by half" because it challenges our intuitive understanding of division. Often, when we hear "divide," we think in terms of reducing the original number. However, dividing by a fraction like 0.5 actually increases the value, which can lead to misunderstandings. This concept is crucial in grasping the overall calculation correctly.
Can You Provide More Examples of Similar Operations?
Absolutely! Understanding similar operations can strengthen your math skills. Here are a few examples:
- Divide 40 by half and add 10:
- 40 ÷ 0.5 = 80
- 80 + 10 = 90
- Divide 30 by half and subtract 5:
- 30 ÷ 0.5 = 60
- 60 - 5 = 55
What is the Importance of Understanding Division by Fractions?
Grasping how to divide by fractions is vital in various fields, including engineering, finance, and everyday life. This understanding helps in calculating proportions, understanding rates, and making informed decisions based on numerical data. Mastery of division by fractions empowers individuals, enhancing their analytical skills and overall comprehension of mathematics.
How Can One Practice Division by Fractions?
To improve your skills, consider the following methods:
- Work through practice problems involving fractions.
- Utilize online math resources and calculators.
- Engage with math games that challenge your division skills.
- Join a math study group or forum to discuss and explore mathematical concepts.
Is There a Real-World Application for This Calculation?
Yes! Understanding how to divide by fractions and perform related calculations can be beneficial in various real-world scenarios. Here are a few examples:
- Cooking: Adjusting recipe quantities often involves dividing and multiplying by fractions.
- Finance: Calculating interest rates or loan payments may require similar operations.
- Construction: Measurements often require precise calculations involving division by fractions.
What Are Common Misconceptions About This Calculation?
Some common misconceptions include:
- Thinking "divide by half" means to simply halve the number, rather than recognizing it as multiplying by 2.
- Assuming the result will always be less than the original number when dividing.
These misconceptions highlight the importance of understanding mathematical operations correctly to avoid errors in calculations.
Conclusion: Divide 50 by Half and Add 20
In conclusion, when you divide 50 by half and add 20, you end up with a total of 120. Recognizing the importance of understanding division by fractions can significantly enhance your mathematical abilities. As we've explored in this article, clarity and practice are key to mastering such calculations. So, the next time you encounter a division involving fractions, remember to think critically about the operation at hand, and you'll be well on your way to solving it with confidence!